ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ В МЕНЕДЖМЕНТЕ
ЛАБОРАТОРНАЯ РАБОТА 8. Решение задач оптимизации средством анализа данных MS Excel Поиск решения.
Цель работы: используя возможности программы Microsoft эффективно планировать экономическую деятельность (решать задачи оптимизации).
Для решения оптимизационных экономических задач Excel содержит процедуру поиска решения. Рассмотрим применение этого средства для решения транспортной задачи.
Пример 1. Предположим, что фирма имеет 4 фабрики по производству товаров и 5 центров распределения этих товаров. Фабрики характеризуются производственными мощностями (количество единиц продукции, произведенных за день), а центры – потребностями в этих товарах (рисунок 57).
Рисунок 57 - 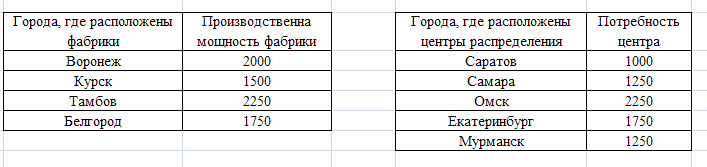
Фабрики и центры распределения товаров расположены в разных городах. Стоимость перевозки единицы продукции между ними (в долларах) известна и приведена на рисунке 58

Рисунок 58 - Стоимость перевозки единицы продукции
Будем считать, что суммарный объём произведённой продукции всеми фабриками равен суммарному объёму потребностей в ней центров распределения. В таком случае фабрики не имеют расходов, связанных со складированием не отгруженной продукции, а центры распределения не имеют издержек, связанных с недопоставками продукции. Т.е. производство и распределение продукции фирмы – сбалансированы. Задача состоит в планировании объемов перевозок таким образом, чтобы минимизировать суммарные транспортные расходы фирмы.
Такие задачи решаются методами линейного программирования, основными из которых являются Симплекс-метод и метод Северо-западного угла и др. В различных пакетах математических программ используются модификации указанных методов, более эффективно использующие возможности компьютерных технологий. В частности, в Microsoft Excel реализована процедура оптимального Поиска решений, которая может быть применена для решения данной задачи.
Построение математической модели.
Для решения данной задачи построим её математическую модель, функцией цели которой являются суммарные транспортные расходы - Z,
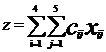
где Cij – стоимость перевозки единицы продукции с i-й фабрики в j-й центр распределения, Xij – объём перевозок с i-фабрики в j-й центр распределения.
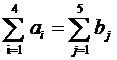
Неизвестными величинами в этой модели является объемы перевозок Xij.. Они должны удовлетворять ограничениям:
Ø Объемы перевозок не могут быть отрицательными: Xij>0.
Ø Объемы перевозок не могут превышать заданных мощностей фабрик и потребностей центров.
![]() Поскольку
строится сбалансированная модель, то не учитываются издержки, связанные
как со складированием, так и с недопоставками продукции. В противном
случае в модель нужно было бы ввести:
Поскольку
строится сбалансированная модель, то не учитываются издержки, связанные
как со складированием, так и с недопоставками продукции. В противном
случае в модель нужно было бы ввести:
Ø В случае перепроизводства – фиктивный пункт распределения, стоимость перевозок единицы продукции в который полагается равной стоимости складирования излишков продукции на фабриках;
Ø В случае дефицита – фиктивную фабрику, стоимость перевозок единицы продукции с которой полагается равной стоимости штрафов за недопоставку продукции, а объём перевозок – объёмам недопоставок продукции в пункты распределения.
Решение задачи с помощью команды ПОИСК РЕШЕНИЯ.
Оформите таблицу «Транспортные расходы на единицу продукции», введите в ее ячейки значения стоимости перевозки единицы продукции – Cij(рисунок 58).
Для записи результатов решения задачи подготовьте ещё одну таблицу «Объемы перевозки».
Установите в ячейках C13:G16 формат для записи целых чисел. Слегка затонируйте их. После решения задачи в ячейках этой таблицы должны появиться искомые величины Xij
Подготовьте ячейки C17:G17. В каждую из них введите функции суммирования значений по столбцам. После решения задачи здесь должны появиться объёмы перевозок в каждый центр распределения. Пока в ячейках находятся нулевые значения. Аналогично введите в ячейки H13:H16 функции суммирования по строкам этой таблицы, вычисляющие объёмы продукции, произведенные каждой фабрикой.
Задайте характеристики фабрик и центров, являющиеся ограничениями для решения задачи:
В ячейки I13:I16 введите значения производственных мощностей фабрик, а в ячейки C18:G18 введите значения потребностей центров распределения.
Отформатируйте введенные значения так, чтобы они хорошо выделялись на листе. Название этих величин впишите в виде примечаний.
Подготовьте ячейку I18 для расчета величины целевой функции - Z. Введите в эту ячейку целевую функцию =СУММПРОИЗВ(C5:G8;C13:G16), указав нужные диапазоны обеих таблиц. Затонируйте ячейку. До проведения каких-либо расчётов результатом этой функции будет 0.
Теперь выберите команду ДАННЫЕ/ПОИСК РЕШЕНИЯ и заполните открывшееся диалоговое окно следующим образом:
|
целевая ячейка |
I18 |
|
равна |
Минимальному значению |
|
изменяемые ячейки |
C13:G16 |
|
ограничения |
Вводятся кнопкой Добавить C13:G16 >= 0 C17:G17 = C18:G18 H13:H16 = I13:I16 |
|
параметры |
Линейная модель |
После нажатия кнопки Выполнить средство Поиска решений находит оптимальный план поставок продукции (объемы перевозок) и минимальные суммарные транспортные расходы (Z=$24312,5)
Сравните свои результаты со значениями таблицы на рисунке 59. Сохраните файл в своей папке.

Рисунок 59 - Решение транспортной задачи
Пример 2. Фабрика имеет в своем распоряжении определенное количество ресурсов: рабочую силу, деньги, сырье, оборудование, производственные площади и т. п. Допустим имеются ресурсы трех видов рабочая сила, сырье и оборудование в количестве соответственно 80 (чел/дней), 480 (кг), 130 (станко/часов). Фабрика может выпускать ковры четырех видов. Информация о количестве единиц каждого ресурса необходимых для производства одного ковра каждого вида и доходах, получаемых предприятием от единицы каждого вида товаров, приведена в таблице на рисунке 60. Требуется найти такой план выпуска продукции, при котором общая стоимость продукции будет максимальная.
|
Ресурсы |
Нормы расхода ресурсов на единицу изделия |
Наличие ресурсов |
|||
|
Ковер А |
Ковер В |
Ковер С |
Ковер D |
||
|
Труд |
7 |
2 |
2 |
6 |
80 |
|
Сырье |
5 |
8 |
4 |
3 |
480 |
|
Оборудование |
2 |
4 |
1 |
8 |
130 |
|
Цена (тыс.руб.) |
3 |
4 |
3 |
1 |
|
Рисунок 60 - Исходные данные задачи
Формулировка математической модели.
Обозначим через x1, x2, x3, x4 количество ковров каждого типа.
Целевая функция 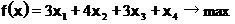
Ограничения по ресурсам
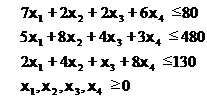
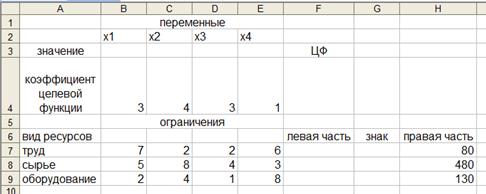
Рисунок 61 - Ввод исходных данных
Ввод зависимости для целевой функции
§ Вызвать Мастер функций fx на панели инструментов Выбрать категорию Математические.
§ Выбрать функцию СУММПРОИЗВ.
§ В массив 1 ввести B3:E3.
§ В массив 2 ввести B4:E4. Готово.
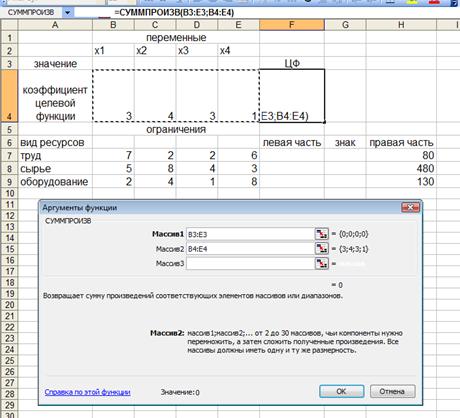
Рисунок 62 - Ввод формул для решения задачи
Ввод зависимостей для ограничений
F7=СУММПРОИЗВ(В3:Е3,В7:Е7)
F8=СУММПРОИЗВ(В3:Е3,В8:Е8)
F9=СУММПРОИЗВ(В3:Е3,В9:Е9)
Запуск Поиск решения
После выбора команд ДАННЫЕ/ПОИСК РЕШЕНИЯ появится диалоговое окно Поиск решения.
В диалоговом окне Поиск решения есть три основных параметра: Установить целевую ячейку; Изменяя ячейки; Ограничения.
При назначении целевой функции и изменяемых ячеек необходимо установить Курсор в поле Установить целевую ячейку / Ввести адрес $F$4 / Ввести направление целевой функции: Максимальному значению / Курсор в поле Изменяя ячейки/ Ввести адреса В$3:E$3.
При вводе ограничений необходимо установить Курсор в поле Добавить / Появится диалоговое окно Добавление ограничения / После ввода последнего ограничения ввести ОК.
При вводе параметров для решения ЗЛП: Открыть окно Параметры поиска решения / Установить флажок Линейная модель / Установить флажок Неотрицательные значения / ОК / Выполнить.
Полученное решение (рисунок 63) означает, что максимальный доход 150 тыс. руб. фабрика может получить при выпуске 30 ковров второго вида и 10 ковров третьего вида. При этом ресурсы труд и оборудование будут использованы полностью, а из 480 кг пряжи (ресурс сырье) будет использовано 280 кг.
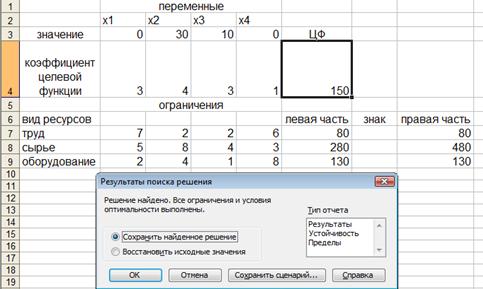
Рисунок 63 - Результаты решения задачи.
Контрольные вопросы:
Ø Для решения каких задач используется процедура Поиска решения?
Ø Для чего применяются ограничения в процессе поиска решений?
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ: